Самое актуальное и обсуждаемое
Популярное
Полезные советы

Важно знать!
Русская кухня
История открытия
Сандуновские бани существуют более 200 лет. Участок земли, на котором они стоят, был куплен на деньги от продажи бриллиантов императрицы Екатерины II. Их она подарила своим придворным...
Читать далее
Калькулятор веса профильной трубы прямоугольного сечения
Из чего делают веники для подметания пола
Инфракрасная сауна. польза и вред, что это, противопоказания, чем полезна. правила посещения при простуде, беременности
Подарочные карты краснопресненских бань
Как сделать шлакоблоки своими руками
Гост 14098-2014 соединения сварные арматуры и закладных изделий железобетонных конструкций. типы, конструкции и размеры (с изменением n 1, с поправкой)
Сп 50.13330.2012 тепловая защита зданий. актуализированная редакция снип 23-02-2003 (с изменением n 1)
Какие камни лучше использовать для бани
Программы для составления плана бани
Рекомендуем
Лучшее

Важно знать!
Гидроизоляция фундамента
Выполнение гидроизоляции ленточного фундамента при закладке
Схема гидроизоляции ленточного фундамента.
При под строение гидроизоляцию его выполняют в несколько этапов.На начальном уровне для гидроизолирующего...
Читать далее
Как выбрать купель для бани
Расчет систем вентиляции
Парилка своими руками
Схемы вязания мочалок для начинающих с описанием работы
Как изготовить буронабивной фундамент
Щитовая баня своими руками
Телескопические доборы на межкомнатные двери и на входные двери как лучший выход для домашнего мастера
Баня по чёрному: фото история в деталях…
Отделка парилки в бане
Новое
Обсуждаемое

Важно знать!
Как сделать из коробки из-под сока кормушку для птиц
Как сделать кормушку для кур своими руками
Изготовить кормушку для домашней птицы можно также из любого материала. Рассмотрим мастер-классы для разного уровня мастерства и сложности.
Бункерная кормушка...
Читать далее
Сауна в квартире: нюансы, требования, получение разрешения, создание собственными руками (53 фото)
Инструкция по применению суперфосфата на огороде: состав, способы использования
Свяжитесь с нами
Баня на колесах своими руками: как сделать, способы реализации проекта и советы экспертов
Как утеплить мансарду изнутри своими руками правильно
Баня по финской технологии
Физалис (70 фото): виды и уход
Фольга для бани: какую лучше выбрать
Как убрать скрип пола не срывая
Актуальное

Важно знать!
Калимагнезия
Выбор средства с учетом особенностей почвы
В калийную группу входят следующие препараты: калия сульфат и хлорид, калий хлористый, калийная соль, поташ, сильвинит, сульфат калия-магния и каинит. Удобрения...
Читать далее
Душица
Что такое абаш для бани
Бани краснодар
Какие камни лучше для бани? обзор кандидатов по всем критериям, отзывы парильщиков и народный рейтинг
Как сделать котел для бани своими руками
Полив орхидей янтарной кислотой
Как установить парогенератор для бани своими руками: используем электрический парогенератор
Джутовая ткань: описание с фото, структура, состав ткани и применение
Японские бани, фурако, офуро
Обновления
 Статьи
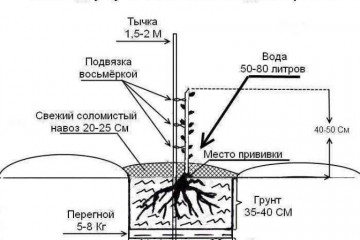
Успешная посадка груш: советы по времени и технике для вашего дачного участка.
Статьи
Успешная посадка груш: советы по времени и технике для вашего дачного участка.
В волнующем мире садоводства, где каждый мгновение приносит новые возможности для создания красивого...
 Статьи
Умное садоводство: почва и уход за саженцами ореха для богатого урожая!
Статьи
Умное садоводство: почва и уход за саженцами ореха для богатого урожая!
В мире садоводства и огородничества саженцы ореха представляют собой не только потенциальный урожай,...
 Статьи
Дизельная электростанция AGG: виды и конструкция дизельных станций
Статьи
Дизельная электростанция AGG: виды и конструкция дизельных станций
Дизельные генераторы стали все более популярными за последние годы, многие отрасли и бизнесы предпочитают...
 Статьи
Как выбрать светильник в квартиру-студию?
Статьи
Как выбрать светильник в квартиру-студию?
Выбор правильной лампы для вашей однокомнатной квартиры может стать непростой задачей. Лампа может...
 Статьи
Какой материал лучше всего подходит для чашек и кружек?
Статьи
Какой материал лучше всего подходит для чашек и кружек?
При выборе чашек и кружек необходимо учитывать несколько особенностей. Во-первых, подумайте о материале....
 Статьи
Модные интерьеры в 2023 году
Статьи
Модные интерьеры в 2023 году
Тенденции в дизайне ремонта домов постоянно развиваются, и популярные тенденции могут меняться в...
 Статьи
Описание и характеристики стальной оцинкованной проволоки по гост
Статьи
Описание и характеристики стальной оцинкованной проволоки по гост
Для чего применяется оцинкованная проволока?
Она применяется для формирования разных тросов, сеток,...
 Статьи
Геотекстиль. что из себя представляет, разновидности и применение
Статьи
Геотекстиль. что из себя представляет, разновидности и применение
Огнеупорный геотекстиль — это тип текстиля, изготовленный из материалов, обработанных для защиты от...
 Статьи
Покупка квартиры в новостройке: инструкция
Статьи
Покупка квартиры в новостройке: инструкция
При выборе квартиры в новостройке в Новосибирске важно учитывать расположение, площадь и особенности...
 Статьи
Рейтинг из топ-7 лучших инфракрасных теплых полов: какие нюансы нужно обязательно учитывать при выборе
Статьи
Рейтинг из топ-7 лучших инфракрасных теплых полов: какие нюансы нужно обязательно учитывать при выборе
Электрические теплые полы — отличный выбор для тех, кто ищет простой и доступный способ обогрева полов. Электрические...
 Статьи
Красивые интерьеры: актуальные тенденции следующего десятилетия
Статьи
Красивые интерьеры: актуальные тенденции следующего десятилетия
Дизайн квартир 2022 года.
Когда люди думают о современном интерьере, они часто представляют...
 Статьи
Заправка туристических газовых баллонов: легко и просто
Статьи
Заправка туристических газовых баллонов: легко и просто
Где заправлять газовые баллоны? И где этого не стоит делать?
Продажа газа для бытовых баллонов осуществляется...